-
Comparisons
-
Hardware Features
-
Systems
-
Software
-
Company
Knowledge-Base
- Hardware Features
- A/D Basics
ADC and Resolution
Digitizers convert the samples of an analog signal into digital values using analog to digital converters (ADCs). The resolution of the ADC is the number of bits it uses to digitize the input samples. For an n bit ADC the number of discrete digital levels that can be produced is 2n. Thus, a 12 bit digitizer can resolve 212 or 4096 levels. The least significant bit (lsb) represents the smallest interval that can be detected and in the case of a 12 bit digitizer is 1/4096 or 2.4 x 10-4. To convert the lsb into a voltage we take the input range of the digitizer and divide by two raised to the resolution of the digitizer. Table 1 shows the lsb for a one Volt (500 mV) input range for digitizers with resolutions of 8 to 16 bits.
| Resolution | Ideal Dynamic range | Minimum Voltage Increment |
|---|---|---|
| 8 Bit | 256:1 | 3.92 mV |
| 10 Bit | 1024:1 | 0.98 mV |
| 12 Bit | 4096:1 | 0.244 mV |
| 14 Bit | 16384:1 | 61 µV |
| 16 Bit | 65536:1 | 15 µV |
Resolution determines the precision of a measurement. The greater the digitizer resolution,the more precise the measurement values. A digitizer with an 8-bit ADC divides the vertical range of the input amplifier into 256 discrete levels. With a vertical range of 1 V, the 8 bit ADC cannot ideally resolve voltage differences smaller than 3.92 mV; while a 16 bit ADC, with 65,656 discrete levels, can ideally resolve voltage differences as small as 15 µV.
One reason to use a high-resolution digitizer is to measure small signals. Based on the way the minimum voltage level was computed we could use a lower resolution instrument and a smaller full scale range to measure smaller voltages. However, many signals contain both small signal and large signal components. Thus, for signals with both large and small voltage components a high-resolution instrument, which has a large dynamic range and the ability of the digitizer to measure small signals and large ones simultaneously, is needed.
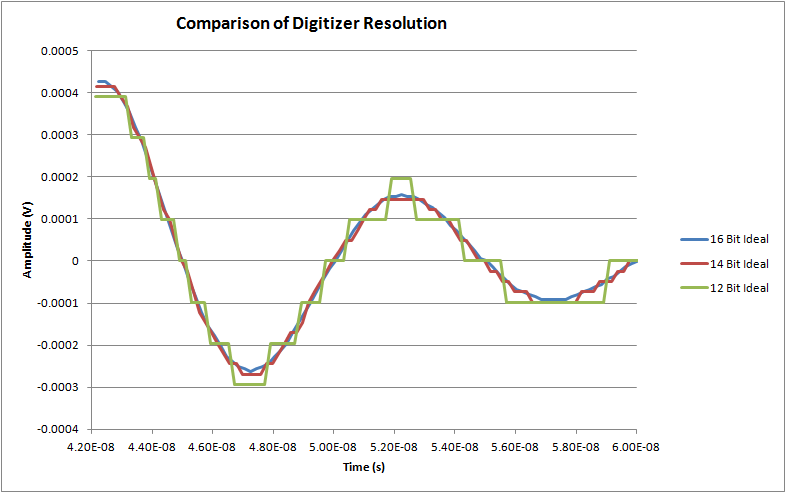 Let us examine how a waveform would look if it is passed through digitizers with different resolutions. Figure 1 compares 12, 14 and 16-bit ideal digitizer responses to a segment of a 200 mV damped sine waveform.
Let us examine how a waveform would look if it is passed through digitizers with different resolutions. Figure 1 compares 12, 14 and 16-bit ideal digitizer responses to a segment of a 200 mV damped sine waveform.
The segment selected is near the end of the waveform and has small amplitude. The 14 and 16 bit digitizers still have sufficient resolution to render the signal accurately but the 12 bit digitizer, with 100 µV resolution (based on a full scale level of 200 mV) is unable to resolve levels smaller than 100 µV. The error in reading, for any resolution, will increase with decreasing signal amplitude. Keep in mind that this is an ideal case, later we will look at issues that limit the accuracy and precision in the real world.