 Self-excited electronics like power supplies, oscillators, transmitters, and signal generators can often be tested using a measuring instrument (digitizer, oscilloscope, spectrum analyzer, etc.) alone. Externally excited electronic devices like amplifiers, filters, receivers, and digital interfaces require a signal source and a measuring instrument for testing. Modular Arbitrary Waveform Generators (AWGs) and modular digitizers are available with multiple source and measurement channels that can be configured in bandwidth, sample rate, and memory. Combining the two products in one system, as shown in Figure 1, provides very cost effective and efficient way to meet an extensive range of test requirements. Figure 1 shows a stimulus/response test system composed of a Spectrum M4i.4451-x8, 500 MS/s, 250 MHz, 14-bit digitizer and an M4i.6631-x8, 1.25 GS/s, 400 MHz, 16 bit, arbitrary waveform generator mounted in a portable computer.
Self-excited electronics like power supplies, oscillators, transmitters, and signal generators can often be tested using a measuring instrument (digitizer, oscilloscope, spectrum analyzer, etc.) alone. Externally excited electronic devices like amplifiers, filters, receivers, and digital interfaces require a signal source and a measuring instrument for testing. Modular Arbitrary Waveform Generators (AWGs) and modular digitizers are available with multiple source and measurement channels that can be configured in bandwidth, sample rate, and memory. Combining the two products in one system, as shown in Figure 1, provides very cost effective and efficient way to meet an extensive range of test requirements. Figure 1 shows a stimulus/response test system composed of a Spectrum M4i.4451-x8, 500 MS/s, 250 MHz, 14-bit digitizer and an M4i.6631-x8, 1.25 GS/s, 400 MHz, 16 bit, arbitrary waveform generator mounted in a portable computer.
A Simple Frequency Response Measurement
The AWG, with its great flexibility in generating almost any waveform, is the key to the test systems effectiveness. Consider a simple test for determining the frequency characteristics of an amplifier or filter. The test requires a signal source with a bandwidth greater than that of the device under test. Furthermore, the source needs to deliver a constant output level over the entire testing bandwidth. A swept sinewave or impulse function waveforms offer broad band output with flat spectral characteristics. Either can be generated by an AWG. The swept sine offers a greater dynamic range for the measurement. Figure 1 shows the result of a swept sine frequency response measurement of a 36 MHz low pass filter. In this example, the data is from a Spectrum Model M4i.4450-x8 500 MS/s, 14-bit digitizer and a Model M4i.6631-x8 1.25GS/s, 16-bit AWG. The data is displayed using Spectrum's SBench 6 instrument software.
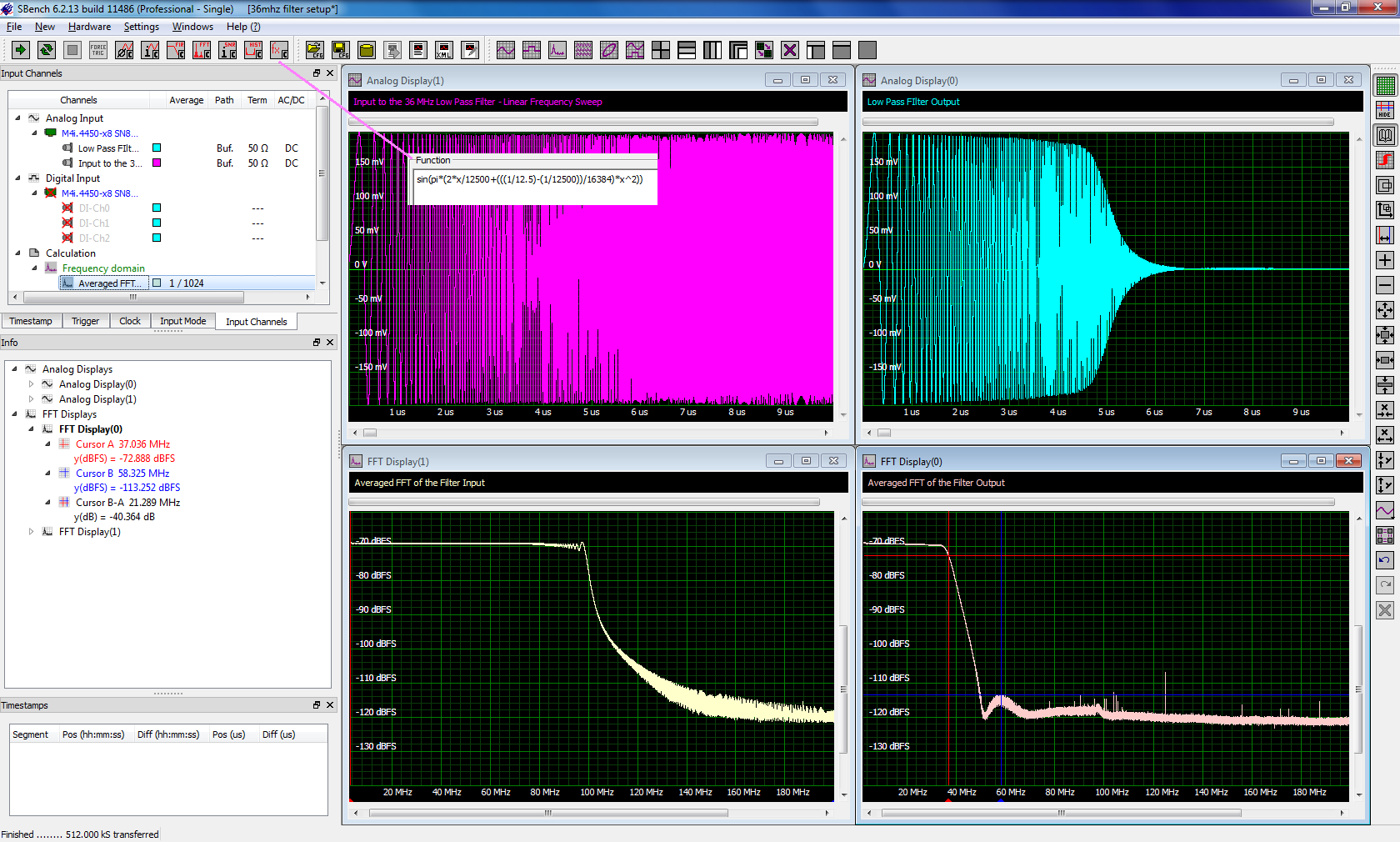 The upper left grid shows the swept sine that was applied to the input of the filter. The signal was created using an equation in the function generator tool in the instance of SBench 6 that controlled the AWG. The inset in the figure shows the equation. The Fast Fourier Transform (FFT) of the filter input is shown in the bottom left grid. The swept sine was flat out to 100 MHz. The time response of the filter to the sweep input is shown in the upper right grid. The filter output decreases rapidly above its 36 MHz cutoff frequency. The matching frequency response is shown in the grid on the lower right. This quantifies the filter bandwidth and shows the in-band flatness and the stop-band attenuation.
The upper left grid shows the swept sine that was applied to the input of the filter. The signal was created using an equation in the function generator tool in the instance of SBench 6 that controlled the AWG. The inset in the figure shows the equation. The Fast Fourier Transform (FFT) of the filter input is shown in the bottom left grid. The swept sine was flat out to 100 MHz. The time response of the filter to the sweep input is shown in the upper right grid. The filter output decreases rapidly above its 36 MHz cutoff frequency. The matching frequency response is shown in the grid on the lower right. This quantifies the filter bandwidth and shows the in-band flatness and the stop-band attenuation.
Device Testing
Suppose you had to match several signal diodes for a project: A simple setup for such a test, utilizing the same digitizers and AWG, is shown in Figure 3.
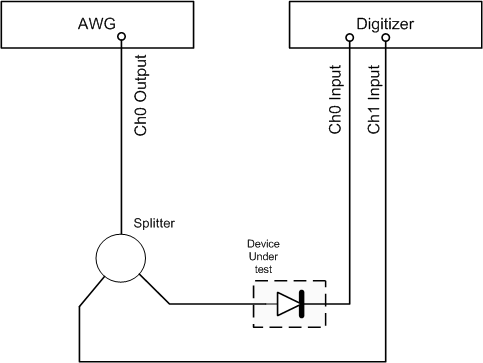 Figure 4 shows the result of the measurement. The AWG is setup to output a ±2 Volt ramp waveform using the Easy Generator tool of SBench 6 (which offers a simple selection of common function generator waveforms). This waveform is applied, through a splitter to the channel Ch1 of the digitizer. The other leg of the splitter is connected to the diode under test and then on to Ch0 of the digitizer. Both channels are set to 50 Ω termination. The voltage on channel Ch0 is proportional to the current through the diode. Rescaling is applied to that channel using SBench 6 so that the readings for Ch0 will be made directly in milli-amperes (mA). The voltage across the diode has to be calculated by subtracting the input voltage of Ch0 from the input voltage on Ch1. This is done using waveform arithmetic in SBench 6. Figure 4 shows the result of the measurement.
Figure 4 shows the result of the measurement. The AWG is setup to output a ±2 Volt ramp waveform using the Easy Generator tool of SBench 6 (which offers a simple selection of common function generator waveforms). This waveform is applied, through a splitter to the channel Ch1 of the digitizer. The other leg of the splitter is connected to the diode under test and then on to Ch0 of the digitizer. Both channels are set to 50 Ω termination. The voltage on channel Ch0 is proportional to the current through the diode. Rescaling is applied to that channel using SBench 6 so that the readings for Ch0 will be made directly in milli-amperes (mA). The voltage across the diode has to be calculated by subtracting the input voltage of Ch0 from the input voltage on Ch1. This is done using waveform arithmetic in SBench 6. Figure 4 shows the result of the measurement.
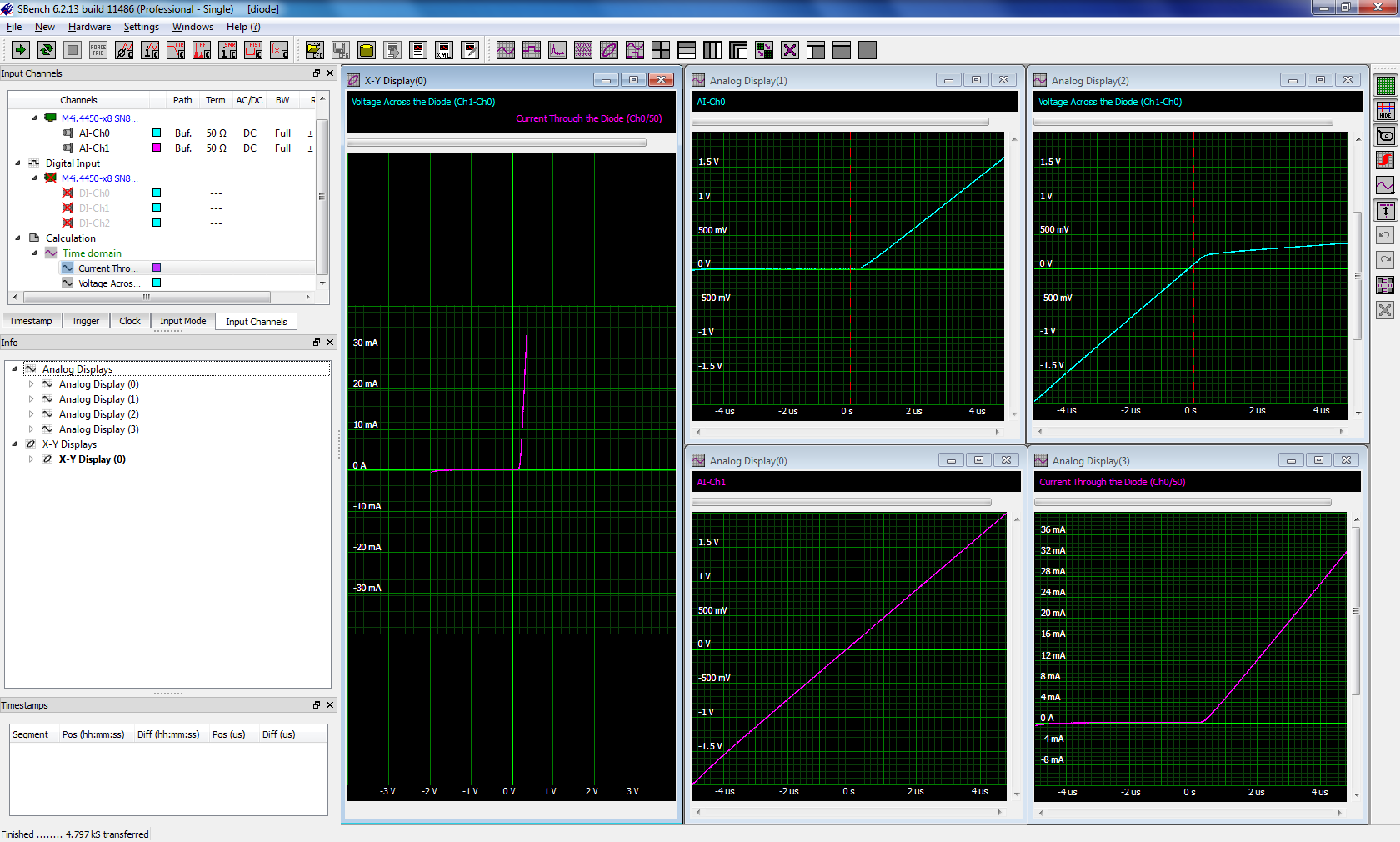 The center bottom grid is the input to Ch1 which is the ramp waveform from the AWG. Above it is the Ch0 waveform which is proportional to the current through the diode. Subtracting Ch0 from Ch1 yields the voltage across the diode shown in the upper right grid. The lower right grid is the rescaled version of CH0 and reads the diode current directly in mA. The X-Y plot in the leftmost grid is the Current-Voltage (I-V) plot of the diode. You can match diodes by verifying that they have closely matched I-V plots.
The center bottom grid is the input to Ch1 which is the ramp waveform from the AWG. Above it is the Ch0 waveform which is proportional to the current through the diode. Subtracting Ch0 from Ch1 yields the voltage across the diode shown in the upper right grid. The lower right grid is the rescaled version of CH0 and reads the diode current directly in mA. The X-Y plot in the leftmost grid is the Current-Voltage (I-V) plot of the diode. You can match diodes by verifying that they have closely matched I-V plots.
Although this is a very simple example of device characterization the AWG/Digitizer system is capable of much more complex small signal device testing. Testing devices at higher voltage and current levels may require amplifiers such as the D/A amplifiers available from Spectrum or similar devices from other vendors.
Replacing or Modelling Missing System Components
In many engineering projects testing can be held up because you are missing a critical component. If you have access to the response waveform of the missing part you can always employ the AWG to provide the part's response to the system. Real world waveforms can be acquired from a digitizer or other instrument and imported into the AWG in any of several file formats depending on the source instrument. Take the controller area network (CANBus) serial data stream from a steering angle sensor shown in Figure 5. This waveform was acquired using an oscilloscope and transferred to the AWG in ASCII file format.
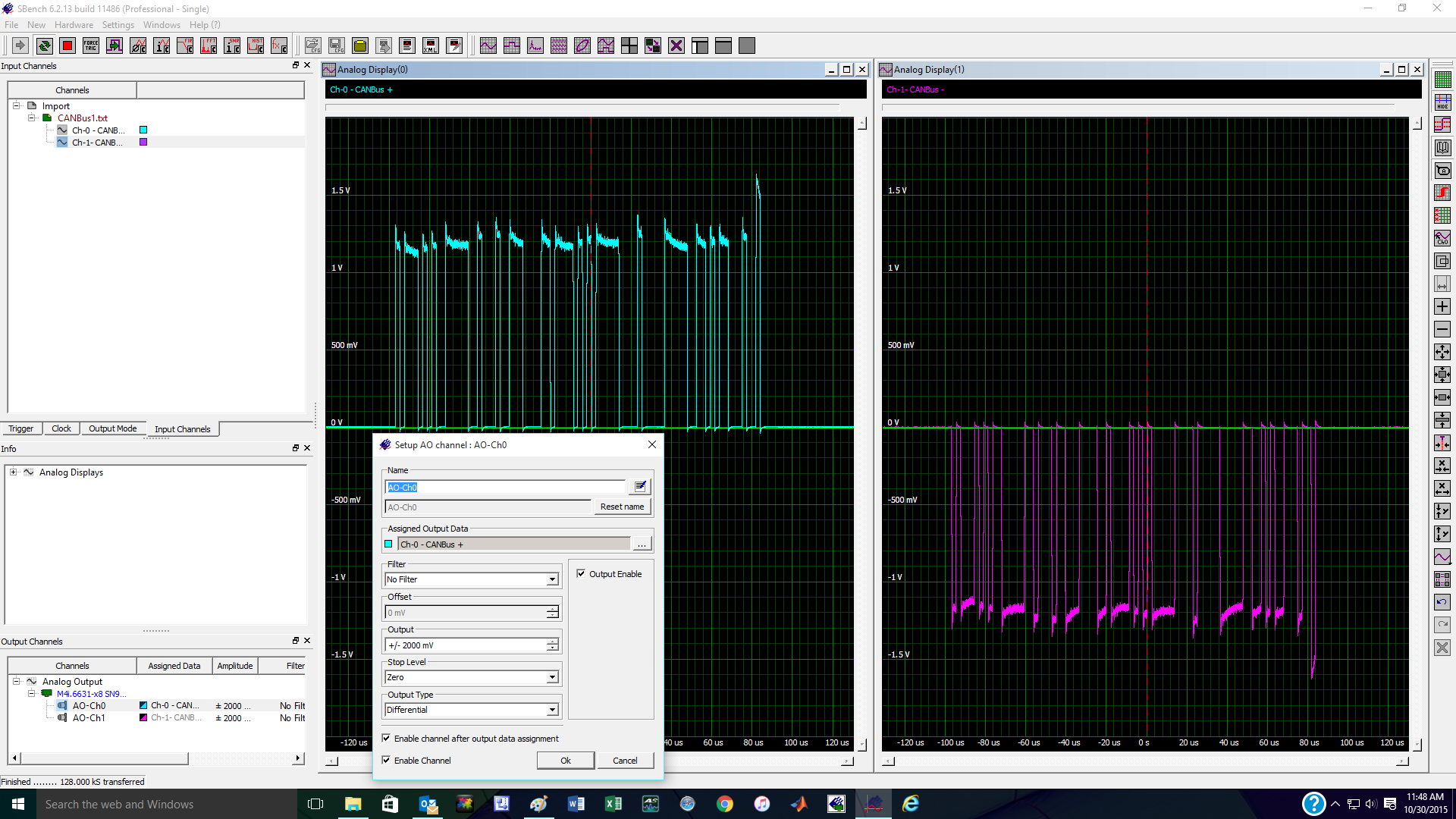 This is a dual channel waveform that represents the differential + and - components of the CANBus signal. Note that the AWG, which has two output channels, is set to output the CANBus waveform as a differential signal.
This is a dual channel waveform that represents the differential + and - components of the CANBus signal. Note that the AWG, which has two output channels, is set to output the CANBus waveform as a differential signal.
This waveform can be output from the AWG upon receipt of a synchronizing trigger when it is required to test the system. Additionally, these waveforms can be modified for margin testing of both amplitude and timing. The AWG used is this example has a real-time sequence mode which allows multiple waveforms, representing a variety of test conditions, which can be output selectively on command and even changed while the test is running. This opens the door to dynamic simulation and testing.
Modulation, Simple and Complex
AWG's can also generate a variety of modulation types for communications testing. Amplitude, phase, and frequency modulation can be achieved as was demonstrated in the first example on frequency response testing where a linear frequency swept sinewave was used. Look at the example shown in Figure 6, where quadrature signal techniques are used to generate a "chirp" waveform at an intermediate frequency (IF).
A chirp is a frequency modulated signal usually associated with RADAR systems. While it could easily be programmed directly as we did in the first example it is instructive to show a general approach that could be used to create other complex modulation.
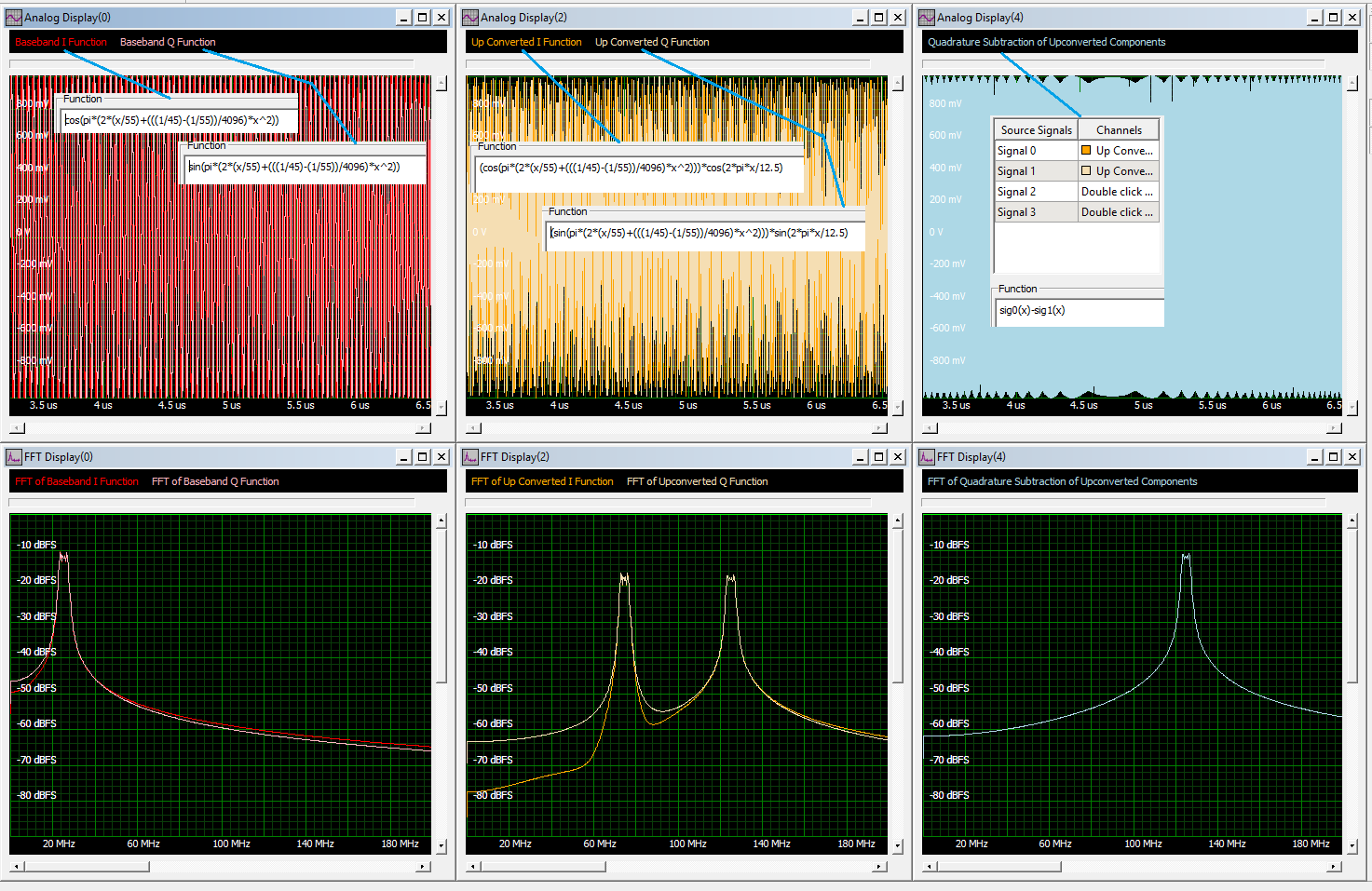 The figure shows the steps in creating the chirp. It starts in the upper left grid where linearly swept sine and cosine waveforms are shown in the time domain along with the equations used to create them. These signals are in quadrature representing the in-phase (I) and Quadrature (Q) components of a quadrature modulation, but the phase difference does not show in the FFT's of these waveforms shown in the lower left grid. The FFT shows the sweep range from 22.7 to 27.7 MHz. This is a baseband signal.
The figure shows the steps in creating the chirp. It starts in the upper left grid where linearly swept sine and cosine waveforms are shown in the time domain along with the equations used to create them. These signals are in quadrature representing the in-phase (I) and Quadrature (Q) components of a quadrature modulation, but the phase difference does not show in the FFT's of these waveforms shown in the lower left grid. The FFT shows the sweep range from 22.7 to 27.7 MHz. This is a baseband signal.
The baseband quadrature components are then up converted by multiplying the I and Q baseband signals by the cosine and sine of the intermediate frequency respectively. The intermediate frequency is 100 MHz. The upper central grid shows the time domain view of the up converted signals. The lower central grid shows the FFT's. Note that the multiplication by a sinusoid has converted the baseband signals to double sideband suppressed carrier signals centered at 100 MHz with upper and lower sidebands extending from 22.7 to 27.7 MHz on either side of the center frequency. What is not seen in the amplitude FFT is the phase of the two quadrature components.
The final step in the process is to do a quadrature subtraction of the two IF components. This occurs in the right hand grids. The lower right grid shows that, as a result of the subtraction, the lower sideband has been cancelled leaving only the upper sideband. This signal sweeps from 122.7 to 127.7 MHz.
This example illustrates how the basic concepts of signal generation and chained processing can be followed to create complex waveforms associated with communications systems.
Conclusion
These few examples show the great diversity that is possible when using an AWG as a signal source for testing. AWG's can generate standard function generator waveforms such as sine, square, triangle and ramp signals. They can generate modulated waveforms and serial data patterns. They can even be used to replay real world signals that have been acquired by digitizers and oscilloscopes. AWG's can be paired with an accompanying digitizer, and programmed using a manufacturer's supplied tool like SBench 6, commonly available system integration software like MATLAB or LabVIEW, or custom programmed in the language of your choice. This flexibility makes modular AWG's and digitizers ideal partners for creating a wide range of stimulus-response (or response-stimulus) testing systems.