Introduction
When selecting a digitizer for acquiring electronic signals the primary specifications considered tend to be sampling rate, bandwidth and resolution. The first two parameters help to define the maximum frequency content that the digitizer will be able to capture. As a general guide for accurate and repeatable measurements users typically try to sample their signal at least ten times faster than its highest frequency content. For example, a 10 MHz signal would be sampled at around 100 MS/s to ensure the digitized signal has sufficient time resolution to be accurately reproduced. Similarly, to be certain that signals are not being unintentionally attenuated (with amplitude information being lost), users generally aim for the digitizers analog bandwidth to be at least two to five times above their highest signal frequency content. So, depending on the test that needs to be made, measuring a 10 MHz signal typically requires a bandwidth of 20 to 50 MHz.
While sample rate and bandwidth are crucial for revealing a signals time and frequency content it’s the third parameter, resolution, which is the most vital for detecting amplitude changes and revealing waveform details. Unfortunately, many people confuse resolution with accuracy, precision and sensitivity. While it certainly has a major impact on these parameters, it does not tell us the full story. Users need to consider all possible sources of digitizer error (such as clock accuracy, distortion, noise and linearity) to understand how well a product will perform when measuring their particular class of signals. To determine the effects of these errors good digitizer manufacturers provide a number of secondary specifications (typically called dynamic parameters) to demonstrate how their models perform under various controlled test conditions.
Understanding Resolution
All digitizer manufacturers specify resolution in bits, which simply tells you how many levels the analog to digital converter (ADC) can discriminate over its full scale (FS) input range. The number of levels is 2n where n is the ADC’s number of bits. As such, an 8 bit ADC has 256 levels while a higher resolution 16 bit ADC has 65,536 levels.
A discrimination level is commonly call a least significant bit (LSB) and is defined by the equation:
1 LSB = FS/2^n
Table 1 summarizes the “theoretical” LSB performance of a range of digitizers with different resolutions from 8 to 16 bits. In this example the full scale range is 1 V. The table shows that the higher resolution ADC’s enable measurements to be made with finer voltage steps. However, it does not indicate what impact any sources of error (such as clock jitter, noise and ADC non-linearity) may have on the “theoretical” performance. To understand the consequences we need to also examine the digitizer’s dynamic parameters and only then can we determine a unit’s real performance.
| ADC Resolution (Bits) | Number of Levels over FS (2n) | Step size (1 LSB) for a 1 V FS range |
|---|---|---|
| 8 | 256 | 3.91 mV |
| 10 | 1024 | 976 uV |
| 12 | 4096 | 244 uV |
| 14 | 16384 | 61 uV |
| 16 | 65536 | 15 uV |
Signal to Noise Ratio (SNR)
Anyone wanting to know how well a digitizer will perform at detecting small (low level) signals that are riding on, or buried in, larger ones needs to examine the digitizers SNR (and not just its resolution). SNR is a measure that compares the amplitude of a desired signal to the amplitude of background noise. SNR is typically expressed in decibels (dB) and calculated by the equation:
SNR(dB) = 10log10 (Psignal/Pnoise)
where P is average power. If you’re measuring the signal and noise amplitude in volts or amperes the proportional power can be obtained by squaring the RMS amplitude measurement:
SNR(dB) = 10log10[(Asignal/Anoise)2]
When considering the dynamic performance and range of a digitizer the SNR, which actually measures the ratio between a signal level (not always the largest one possible) and noise, generally provides a more realistic value than a units “theoretical” LSB. It’s also important to understand that the SNR will vary depending on the input signals. As such, to provide an indication of how well a digitizer will perform, manufactures should measure SNR with well-defined reference signals under a variety of test conditions.
Table 2 shows an example of the SNR measurements made by Spectrum Instrumentation when testing a model M4i.4451-x8, 500 MS/s, 14 bit digitizer (Figure 1) in manufacturing. Note that the measurements are made using 3 different signal frequencies (10, 40 and 70 MHz) and with different full-scale ranges. These measurements allow users to quickly determine the performance that they may expect under similar test conditions and then consider the implications when using their own specific signals. More results for different setups may be available upon request to the manufacturer.
| Test signal Frequency | 10 MHz | 10 MHz | 10 MHz | 10 MHz | 40 MHz | 70 MHz |
|---|---|---|---|---|---|---|
| Input Range | ±0.5 V | ±1 V | ±2.5 V | ±5 V | ±1 V | ±1 V |
| SNR (typ) | >67.8 dB | >67.9 dB | >68.0 dB | >68.0 dB | >69.5 dB | <-67.5 dB |
| SFDR (typ), excl. harm. | >88.1 dB | >88.6 dB | >85.2 dB | >85.3 dB | >88.0 dB | >87.8 dB |
| SFDR (typ), incl. harm. | >80.1 dB | >80.0 dB | >77.4 dB | >77.3 dB | >74.0 dB | >69.9 dB |
| THD (typ) | <-75.9 dB | <-75.8 dB | <-75.2 dB | <-74.8 dB | <-72.5 dB | <-67.4 dB |
| SINAD/THD+N (typ) | >67.2 dB | >67.2 dB | >67.2 dB | >67.2 dB | >67.7 dB | >62.4 dB |
| ENOB based on SINAD | >10.9 bit | >10.9 bit | >10.9 bit | >10.9 bit | >10.9 bit | >10.4 bit |
| ENOB based on SNR | >11.0 bit | >11.0 bit | >11.0 bit | >11.0 bit | >11.0 bit | >10.9 bit |
Spurious Free Dynamic Range (SFDR)
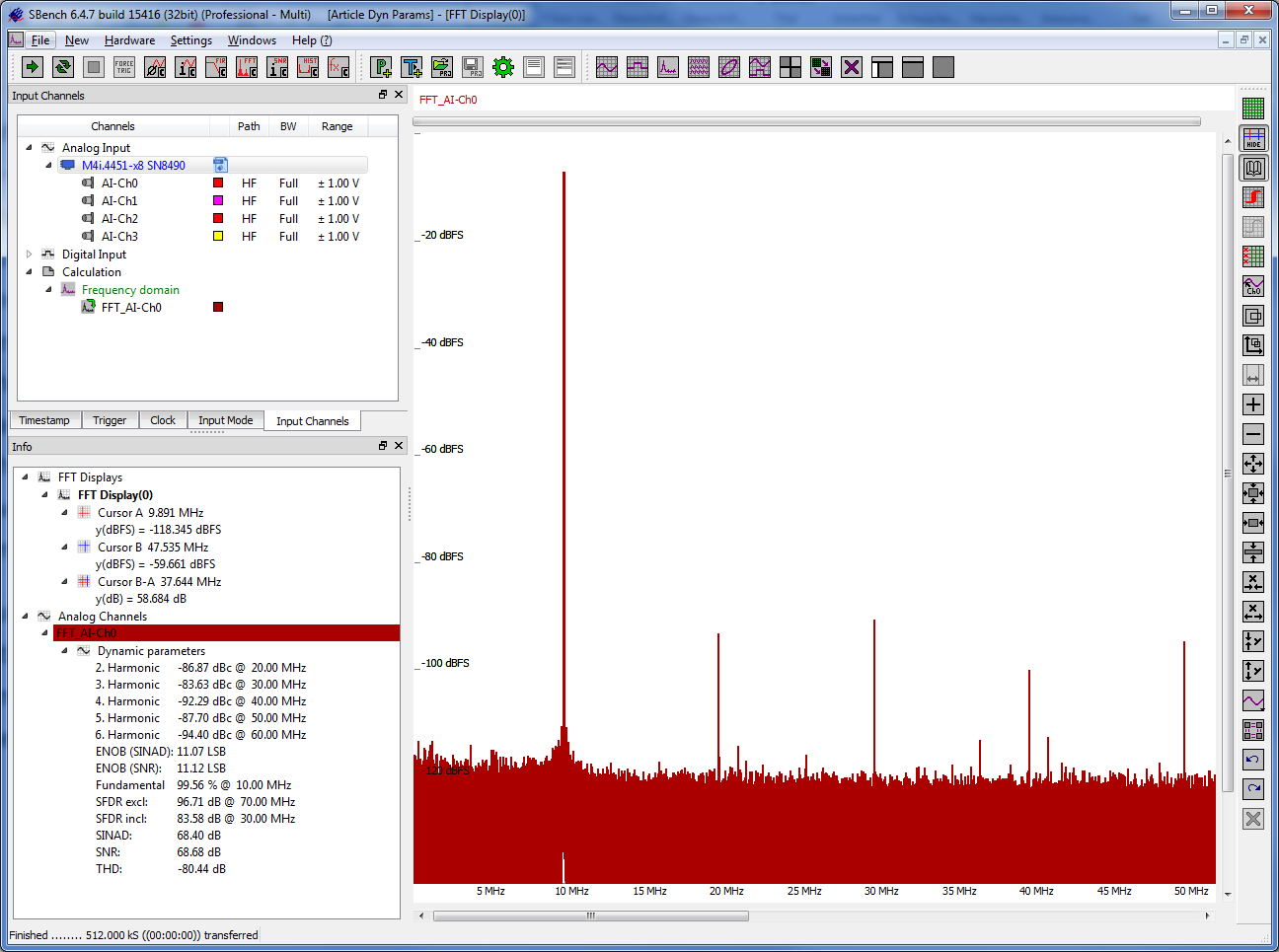Another key performance parameter to consider when determining the suitability of a digitizer to detect low level signals is its SFDR. A spurious signal is any signal component that’s present in the measured waveform that was not present in the input one. The spurious component is an abnormality and it is commonly something that is generated by the digitizing device itself. Manufacturers typically determine SFDR by inputting a pure sine wave, digitizing it, and then examining it in the frequency domain using a Fast Fourier Transform. The SFDR is then measured by looking at the difference, expressed in dB, between the RMS values of the pure sine wave and the peak spurious signal. SFDR is important as it provides a clear indication of the smallest value of signal that can be distinguished from a larger signal.
Figure 2 shows an SFDR measurement made using the Spectrum M4i.4451-x8 digitizer. Furthermore, SFDR measurements can be made with and without the harmonics of the input signal. Table 2 shows the SFDR results obtained under a variety of different test conditions.
Total Harmonic Distortion (THD)
Just how well a digitizer can capture and reproduce a signal also depends on how much waveform distortion results in the process. As the signal passes through the units’ major components, such as the signal conditioning circuitry (amplifiers and attenuators) and the ADC itself, it’s subject to the effects of non-linearity and filtering. To understand the degree to which a signal may be distorted, digitizer manufacturers typically provide a measure of the units THD. Like SNR and SFDR, THD is normally measured by using a variety of pure reference signals. It’s then determined by examining the ratio of the RMS amplitude of a set of higher harmonic frequencies to the RMS amplitude of the reference signals fundamental frequency. The value is calculated using the equation:
THD = Σ harmonic powers/fundamental frequency power = (P2 + P3 + P4 +….+Pn)/P1
Table 2 shows the THD results obtained under a variety of different test conditions for the Spectrum M4i.4451-x8 digitizer.
Harmonics of fast input signals that exceed the FFT bandwidth of ½ of the sampling rate are seen as mirrored signals into lower frequencies. Typically, an overall of 6 harmonics is taken into the calculation as higher harmonic content is not visible above the noise level.
The dynamic parameters SNR, SFDR and THD all measure a different aspect of digitizer performance. To determine the collective impact of these parameters users should also examine some additional specifications.
Signal to Noise and Distortion Ratio (SINAD)
The SINAD (sometimes also called THD+N) parameter is useful as it looks at both SNR and distortion by measuring the ratio of total received power (typically from a reference signal) to the noise-plus-distortion power. It can be calculated form the equation:
SINAD = (Psignal + Pnoise + Pdistortion)/(Pnoise+ Pdistortion)
Table 2 shows the SINAD results obtained under a variety of different test conditions for the Spectrum M4i.4451-x8 digitizer.
Effective Number of Bits (ENOB)
Perhaps one of the most valued dynamic parameters is the digitizers ENOB. This figure of merit aims to compare the measured performance of the digitizer (which includes all the elements of the signal path) against that of an ideal ADC. The ENOB figure is useful as it combines possible sources of error (clock jitter, noise, distortion, etc.) in the final result. ENOB can also be calculated from the SINAD using the equation:
ENOB = (SINAD – 1.76)/6.02
As the resulting ENOB figure is in bits it can immediately be compared to the digitizers stated resolution. Table 2 shows the measured ENOB figures for the Spectrum M4i.4451-x8 digitizer, again under a number of test conditions. As ENOB is sometimes given based on SNR only, without taking the THD component into account, it is good to have both figures for comparison.
Here it is important to understand that ENOB can be heavily influenced by the frequency of the input test signals. As the frequency increases ENOB generally decreases. So, when comparing different digitizers it’s crucial to examine their ENOB under similar test conditions. That said many users are surprised to find that some digitizer products give up a lot of effective resolution as the frequency increases. This can often be due to a unit’s poor design. If parameters such as clock jitter, noise and distortion are not well controlled then it’s not unusual for a digitizer to have an ENOB that’s barely half of the stated resolution of its ADC.
Unfortunately, even though ENOB is a useful figure of merit, it shouldn’t be considered the final word when it comes to digitizer performance. ENOB doesn’t include all possible sources of error. For example, it excludes DC specifications, such as offset and gain error. It also doesn’t take into account other digitizer phenomena, such as cross-talk when using multiple channels, which may impact on a specific measurement.
Reproduce manufacturer’s measurements
When testing a demonstration device, or after purchasing a unit, you may want to reproduce the measurements of the manufacturer to compare your digitizer with the specifications and to judge about the digitizer performance by yourself. Often manufacturers offer basic measurement software that can perform the calculations of SNR, THD and SFDR. Alternatively, you may want to use 3rd party tools for this. Be aware that you always measure the quality of the complete signal chain of signal source, cables and digitizers. This is important especially when looking at high-resolution digitizers. Off-the-shelf signal generators never reach a high enough performance level that they can be directly used as a test signal source.
Digitizer manufacturers all use additional high-performance band-pass filters to get a pure sine signal with as little additional noise and distortion as possible out of a signal generator. To copy their measurements, you’d need the same level of device for every test signal frequency.
Maximizing measurement performance
Obviously if accuracy, precision and sensitivity are important then choosing a digitizer with the best dynamic parameter specifications is a good start. However, there are also a few helpful tips that can have a big impact on the final results. Here are five simple ones:
- Always maximize the signal being analyzed so that it covers as much of the input range of the digitizer as possible. This maximizes the signal to noise ratio by using more of the ADCs dynamic range. Selecting a digitizer with multiple input ranges makes this much easier but make sure the noise level doesn’t simply scale with any applied attenuation or amplification.
- Use the minimum measurement bandwidth consistent with the application. Noise level is proportional to bandwidth. This can be implemented using input bandwidth limiting or with digital filtering.
- Use signal processing such as averaging to reduce the noise level proportional to the number of measurements averaged. Keep in mind this requires a repeatable signal and multiple acquisitions.
- For low level signals use external “low noise” amplifiers to boost the signal level and maximize the signal to noise ratio.
- Use the proper termination in the complete signal path. For high bandwidth applications a complete 50 Ω termination for signal source, cabling and digitizer termination is a good choice.
Conclusion
When choosing a digitizer for a specific application look beyond the banner specifications of sampling rate, bandwidth and resolution if you wish to ensure the product can perform the measurement task you require. Dynamic parameters SNR, SFDR, THD, SINAD and ENOB all reveal information about how well the product will work under specific conditions. Consider your expected signals and examine the dynamic parameters (that should have been measured under similar frequency and amplitude ranges as your signals) to ensure they meet or exceed your requirements. Don’t trust single figures that are given without any background information on how they have been measured. Only then should you have confidence that the product will deliver the desired measurement results in your environment.