Two of the key specifications of digitizers are bandwidth and amplitude resolution. These specifications are not independent - with increasing resolution available with decreasing bandwidth. Users must make a tradeoff in selecting a digitizer to meet their measurement needs. This article discusses the advantages and limitations of high resolution in high bandwidth digitizers. Where high resolution is greater than 12 bits and high bandwidth is greater than 20 MHz.
Resolution and Dynamic Range
Digitizers convert the samples of an analog signal into digital values using analog to digital converters (ADCs). The resolution of the ADC is the number of bits it uses to digitize the input samples. For an n bit ADC the number of discrete digital levels that can be produced is 2n. Thus, a 12 bit digitizer can resolve 212 or 4096 levels. The least significant bit (lsb) represents the smallest interval that can be detected and in the case of a 12 bit digitizer is 1/4096 or 2.4 x 10-4. To convert the lsb into a voltage we take the input range of the digitizer and divide by two raised to the resolution of the digitizer. Table 1 shows the lsb for a one Volt (±500 mV) input range for digitizers with resolutions of 8 to 16 bits.
| Resolution | Ideal Dynamic range | Minimum Voltage Increment |
|---|---|---|
| 8 Bit | 256:1 | 3.92 mV |
| 10 Bit | 1024:1 | 0.98 mV |
| 12 Bit | 4096:1 | 0.244 mV |
| 14 Bit | 16384:1 | 61 μV |
| 16 Bit | 65536:1 | 15 μV |
Resolution determines the precision of a measurement. The greater the digitizer resolution,the more precise the measurement values. A digitizer with an 8-bit ADC divides the vertical range of the input amplifier into 256 discrete levels. With a vertical range of 1 V, the 8 bit ADC cannot ideally resolve voltage differences smaller than 3.92 mV; while a 16 bit ADC, with 65,656 discrete levels, can ideally resolve voltage differences as small as 15 μV.
One reason to use a high-resolution digitizer is to measure small signals. Based on the way the minimum voltage level was computed we could use a lower resolution instrument and a smaller full scale range to measure smaller voltages. However, many signals contain both small signal and large signal components. Thus, for signals with both large and small voltage components a high-resolution instrument, which has a large dynamic range and the ability of the digitizer to measure small signals and large ones simultaneously, is needed.
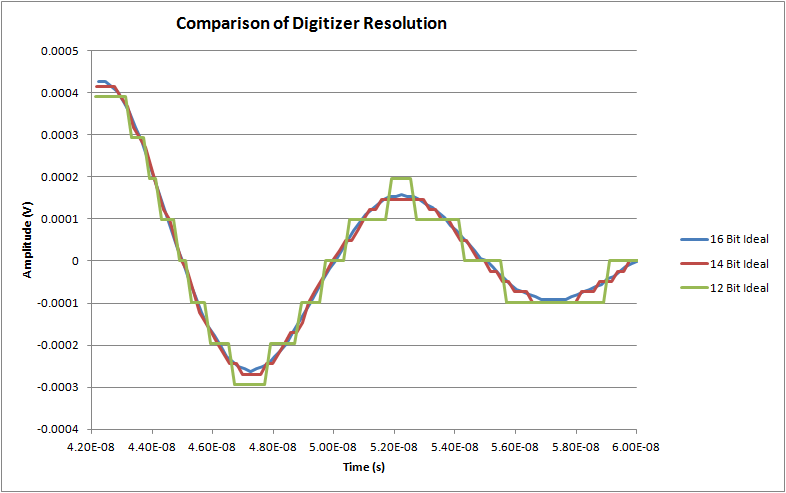Let us examine how a waveform would look if it is passed through digitizers with different resolutions. Figure 1 compares 12, 14 and 16-bit ideal digitizer responses to a segment of a ±200 mV damped sine waveform.
The segment selected is near the end of the waveform and has small amplitude. The 14 and 16 bit digitizers still have sufficient resolution to render the signal accurately but the 12 bit digitizer, with 100 μV resolution (based on a full scale level of ±200 mV) is unable to resolve levels smaller than 100 μV. The error in reading, for any resolution, will increase with decreasing signal amplitude. Keep in mind that this is an ideal case, later we will look at issues that limit the accuracy and precision in the real world.
Resolution vs Sample Rate
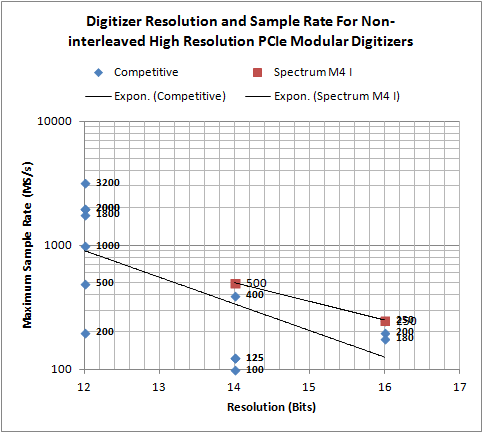Note, as mentioned earlier, there is a tradeoff between resolution and maximum sample rate and hence bandwidth. Higher resolution comes at the price of lower maximum sample rate. This is shown in Figure 2 where the maximum sample rate for a number of competitive modular digitizers is plotted as a function of the number of bits of resolution. The 14 and 16 bit models of the Spectrum M4i series are plotted showing their higher effective sampling rate.
Limitations on Achieving Maximum Resolution
There are several sources of error in digitizer systems. These sources can, in the simplest case, be broken down into noise and distortion.
Distortion is an error in the acquired waveform that is highly correlated with the signal being measured. Distortion is not random, but is dependent on the input signal. The most common form of distortion is harmonic distortion. In the case of harmonic distortion, the distortion components appear, in the frequency domain, at integer multiples of the input frequency. Typical sources of harmonic distortion are non-linearity of the transfer function of the digitizer system including saturation, clipping, slew-rate limiting and others. Digitizer configurations that interleave multiple ADCs to achieve higher sampling rates add significant distortion at the sampling frequency due to mismatches in the gain and offset of each ADC. This is interleaving distortion.
Noise, as opposed to distortion, is assumed to be uncorrelated with the input. Noise can be defined as any portion of the error signal whose frequency locations are not functions of the input frequency. Noise itself is commonly broken into categories depending on the distribution of the noise (i.e. the shape of the histogram of the error) or the shape of the noise spectrum.
When categorized based on frequency domain shape, noise that is evenly spread across all frequencies is called white noise. Noise that is distributed such that the noise power per octave is constant is called pink noise. There are many other noise shapes.
Noise is also categorized by distribution of its histogram. Noise with a normal distribution is called Gaussian noise. There are many sources of Gaussian noise. Noise is also created through quantization - effectively the round-off error in converting analog voltages to digital numbers. The simplest quantization methods produce a uniform error distribution that is white.
Noise arises in all electronic devices and designers make every effort to decrease noise added to the input signal. Gain stages are particularly prone to generate and increase the level on noise in a digitizer.
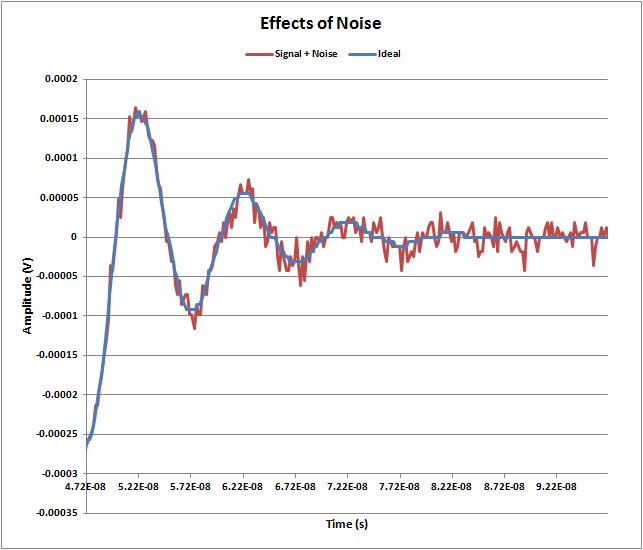
Both distortion and noise limit the resolution which can be achieved by a digitizer. Noise, by adding a random component to each sample value limits the digitizers ability to resolve small amplitude values. This can be seen in Figure 3. This is the same damped sine signal waveform as in Figure 1 but the signal, with and without amplitude noise, is compared in the time domain.
The trace with additive noise shows amplitude transitions that exceed the signal peak amplitudes on the right hand side of the displayed waveform obscuring the actual signal structure. As the noise level increases it will obscure signal components with still higher amplitude values further reducing the resolution of the measurement.
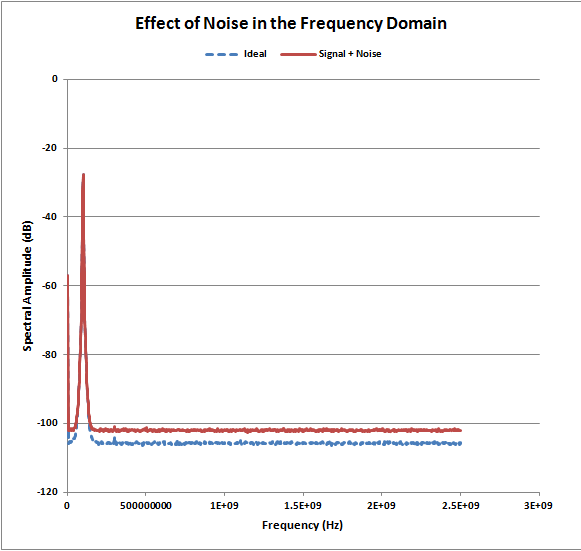
Similarly, the frequency domain spectrum of the damped sine signal, with and without additive white noise, is shown in Figure 4. Note that the addition of the spectrally flat noise raises the baseline of the spectrum. Any signals with amplitude lower than that noise floor will be obscured effectively limiting the dynamic range of the digitizer.
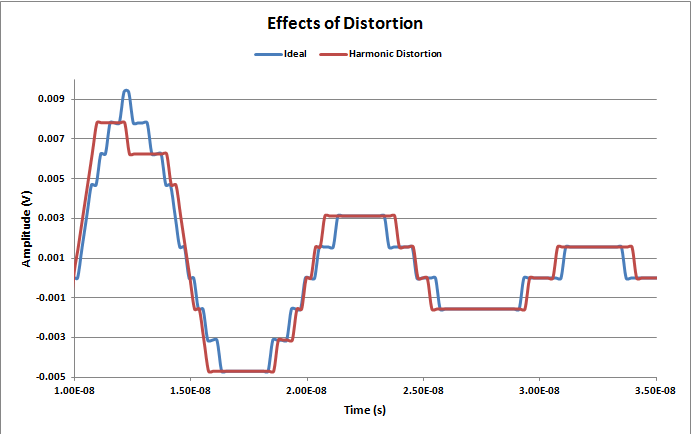
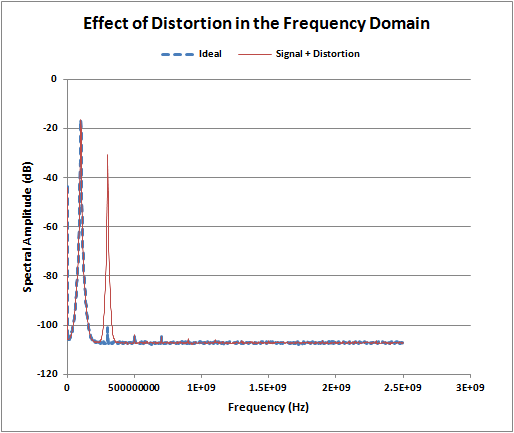Figure 5 show the effect of harmonic distortion on the digitized waveform. In this example a relatively large third harmonic (20%) changes the shape of the digitized waveform. As mentioned earlier, distortion, synchronous with the source waveform, adds in a repeatable manner. Normally, harmonic distortion occurs with much lower levels and is not visible on the time domain waveform. Harmonics are generally evaluated in the frequency domain using a spectrum analyzer of Fast Fourier Transform (FFT) as shown in Figure 6. In the frequency domain you can see the 3rd harmonic clearly. The presence of harmonic and other distortion can hide smaller spectral features which limit the dynamic range of the digitizer. One measure of the spectral purity of a digitizers output is the spurious free dynamic range (SFDR). SFDR is defined as the ratio of the RMS signal frequency component to the RMS value of the next larger spectral component (often referred to as a "spurious" or a "spur") at its output. The ideal spectrum in Figure 6 has a SFDR of about 81 dB.
Minimizing the Effects of Noise and Distortion
Minimizing the effects of distortion is primarily the function of the digitizer designer. Non-linearity, harmonic distortion, and other sources of distortion must be reduced in the design. The user has little control over reducing distortion other than not overdriving the digitizer.
The user has some control over minimizing the effects on noise. Here are some simple tips:
- Maximize the signal being analyzed in the input range of the digitizer. This maximizes the signal to noise ratio. Digitizers with multiple ranges make this easier but make sure the noise level doesn't scale with input attenuation.
- Use the minimum measurement bandwidth consistent with the application. Noise level is proportional to bandwidth. This can be implemented using input bandwidth limiting or with digital filtering.
- Use signal processing such as averaging to reduce noise level proportional to the number of measurements averaged. Keep in mind this requires a repeatable signal and multiple acquisitions.
- For low level signals use external low noise amplifiers to boost signal level and maximize signal to noise ratio.
- Use the proper termination in the complete signal path. For high bandwidth a complete 50 ohm termination for signal source, cabling and digitizer termination is a good choice.
Comparing Digitizers Noise and Distortion Performance
Figures of Merit are measurements for which there are common definitions such that numerical values instantly convey the quality of the measurement system being described.
| Figure of Merit | Abbreviation | Description |
|---|---|---|
| Baseline Noise | RMS noise level, expressed in Volts, with no signal applied. | |
| Total Harmonic Distortion | THD | The ratio of the RMS sum of the significant harmonics to the RMS value of the fundamental expressed in dB. |
| Signal to Noise Ratio | SNR | The ratio of the RMS signal amplitude to the RMS sum of all other spectral components other than distortion and offset error expressed in dB. |
| Signal to Noise and Distortion Ratio | SINAD THD+N | The ratio, expressed in dB, of the RMS signal to the RMS sum of all other spectral components, including the harmonics except DC. |
| Effective number of Bits | ENOB | ENOB is the number of bits in a digitizer that produces the same SINAD value as a system whose only source of noise is quantization itself. |
| Spurious FreeDynamic Range | SFDR | The ratio of the RMS signal frequency component to the RMS value of the next larger spectral component expressed in dB. |
All these figures of merit other than baseline noise are based on frequency domain analysis of the digitizer output for a sinusoidal input. They are defined in IEEE Standards 1057 and 1241. Most digitizer suppliers specify these values in their data sheets (reference 1). When comparing figures of merit, make sure that they are specified for the same input frequency, input amplitude, sample rate, and bandwidth.
Applications Requiring Digitizers with High Dynamic Range
Applications that require digitizers with a large dynamic range and hence greater resolution are those where the signals encountered include both high and low amplitude components. Typical applications include:
- Echo Ranging- Echo ranging measurements such as radar, sonar, lidar, ultrasound and medical imaging. In these applications a large transmitted pulse is followed by a much weaker return echo(s) and the digitizer must be capable of accurately handling both amplitude signals.
- Ripple Measurements- require measurement of signals with high offset values and small variations riding on top of the offset. Both components need to be characterized.
- Modulation analysis- Amplitude modulated signals (AM, SSB, QAM, etc.) exhibit wide variations in signal amplitude
- Mass spectrometry, where particles with significantly different mass/charge ratio need to be detected or the sensitivity of the mass spectrometer needs to be improved.
- Phase measurements - Phase measurements require measurements of very small differences in amplitude to distinguish between small phase differences
- Propagation studies - Measuring signal path attenuation over various paths and through different media often result in large range of amplitude values.
- Component testing, where large voltage or current drops need to be characterized.
Measurement Example
Our measurement example utilizes a Spectrum Instrumentation M4i series digitizer (Figure 7). Figure 8 shows an example of measurement using a 14 bit Spectrum Instrumentation M4i digitizer. Its ENOB specification is >11.6 bits at 10 MHz. Superimposed on that measurement is a simulation of a digitizer with an ENOB of 10 bits. This data is shown graphically using Spectrum's SBench software.
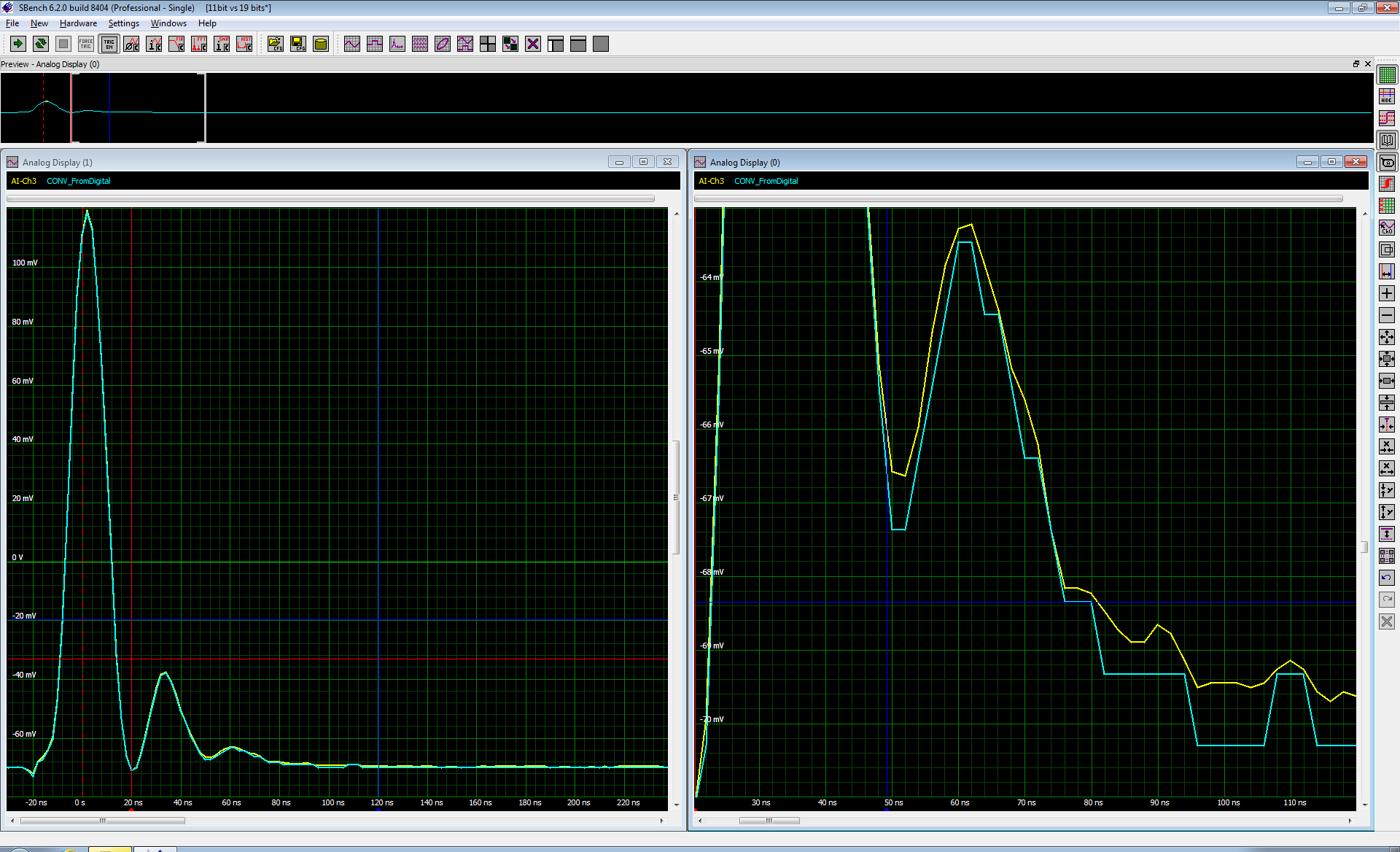Both measurements are shown as acquired in the left hand grid, the Spectrum digitizer trace is shown in yellow, the other trace is in blue. The right hand grid is the same data expanded both horizontally and vertically. Note that the blue trace fails to show the low amplitude details due to its more limited resolution.
Conclusion
Digitizers specify an ideal resolution based on the number of bits in the ADC. This ideal resolution is reduced due to the presence of noise and distortion products. The real resolution is specified in the form of baseline noise, SNR, SINAD, and ENOB. When selecting a digitizer you must match the digitizers true resolution to your measurement needs. You must also keep in mind the hardware tools incorporated into its design like low noise components and layout, multiple input ranges, specialized signal paths, and signal conditioning. With all these in mind you can safely choose the right digitizers for your job.