Boxcar averaging function enhances high-resolution Digitizers
 Analog Boxcar Averaging (sometimes referred to as Gated Integration) is a technique that has been used by engineers and scientists for more than 50 years to reduce unwanted noise on signals. In more recent times, with the development of fast high-resolution digitizer technology, digital Boxcar Averaging has been used to achieve the same type of results. Furthermore, digital Boxcar Averaging brings with it additional benefits in that it can improve a digitizer's overall resolution and its dynamic performance. This white paper shows how digital Boxcar Averaging can be used to reduce signal noise, even on single shot events. It also explains how the function improves a digitizer's resolution and dynamic characteristics such as, effective number of bits (ENOB), signal-to-noise ratio (SNR) and spurious free dynamic range (SFDR).
Analog Boxcar Averaging (sometimes referred to as Gated Integration) is a technique that has been used by engineers and scientists for more than 50 years to reduce unwanted noise on signals. In more recent times, with the development of fast high-resolution digitizer technology, digital Boxcar Averaging has been used to achieve the same type of results. Furthermore, digital Boxcar Averaging brings with it additional benefits in that it can improve a digitizer's overall resolution and its dynamic performance. This white paper shows how digital Boxcar Averaging can be used to reduce signal noise, even on single shot events. It also explains how the function improves a digitizer's resolution and dynamic characteristics such as, effective number of bits (ENOB), signal-to-noise ratio (SNR) and spurious free dynamic range (SFDR).
Digital Boxcar Averaging works in situations where a digitizer samples waveforms at rates that are well above the maximum frequency of a signal to be analyzed, a process commonly referred to as "oversampling". When signals or waveforms are oversampled the Boxcar Averaging function can be used to take advantage of the information available in the oversampled data points. The method employs a mathematical process that effectively sums a selected number of adjacent points (the points in the Boxcar, or the Boxcar Averaging factor) and then calculates an averaged vertical value (the summed result divided by the number of points in the Boxcar). The averaged value is then used to replace all the points in the original Boxcar of data. The resulting operation is similar to applying a smoothing function to the raw digitized data. But unlike smoothing, the final result is a waveform with reduced data points.
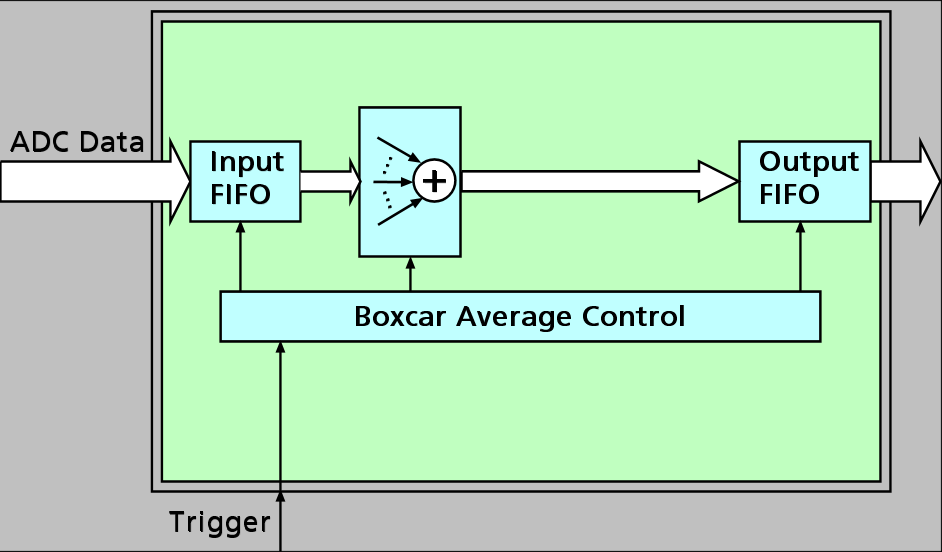 To allow users to take advantage of the Boxcar Averaging function Spectrum Instrumentation has created a new firmware package that can perform the routine using the on-board FPGA technology of its high-resolution 44xx series, 14 and 16 Bit, PCIe, PXIe and LXI digitizer cards and instruments. An example of the PCIe digitizer M4i.4451-x8 which was used for all tests is shown in figure 1. The Boxcar Average package enhances the already high performance of these products and produces results with more vertical resolution, better sensitivity and improved dynamic performance. The Boxcar Averaging firmware is included as standard with all new 44xx series digitizers and can also be retrofitted to existing units that are already in the field.
To allow users to take advantage of the Boxcar Averaging function Spectrum Instrumentation has created a new firmware package that can perform the routine using the on-board FPGA technology of its high-resolution 44xx series, 14 and 16 Bit, PCIe, PXIe and LXI digitizer cards and instruments. An example of the PCIe digitizer M4i.4451-x8 which was used for all tests is shown in figure 1. The Boxcar Average package enhances the already high performance of these products and produces results with more vertical resolution, better sensitivity and improved dynamic performance. The Boxcar Averaging firmware is included as standard with all new 44xx series digitizers and can also be retrofitted to existing units that are already in the field.
How does Boxcar Averaging work?
As mentioned above, the Boxcar Averaging process is similar to a smoothing operation. In its simplest application the function can be used to reduce unwanted noise by acting like a low pass filter and removing high frequency noise components from signals.
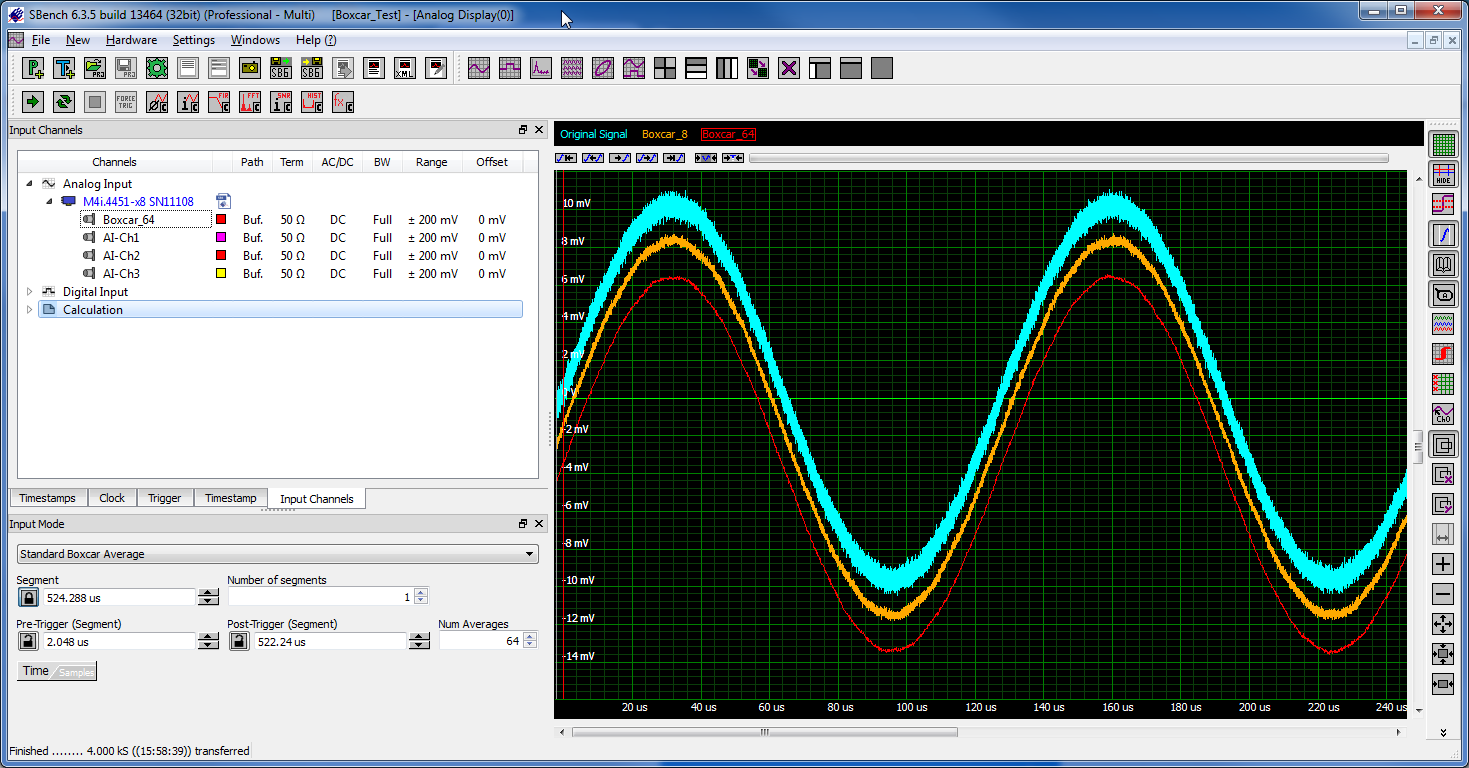 As an example, consider the waveforms shown in Figure 3. The top trace (blue) shows a relatively slow sine wave with a significant level of noise. The waveform was acquired and oversampled using by an M4i.4451-x8 digitizer (figure 1) with a resolution of 14 Bits and a single shot sampling rate of 500 MS/s. The blue trace shows the raw data. The middle trace (orange) and lower trace (red) show the effect of applying Boxcar Averaging functions to the raw data using 8 and 64 adjacent points respectively. Both of the averaged traces display visibly lower noise levels.
As an example, consider the waveforms shown in Figure 3. The top trace (blue) shows a relatively slow sine wave with a significant level of noise. The waveform was acquired and oversampled using by an M4i.4451-x8 digitizer (figure 1) with a resolution of 14 Bits and a single shot sampling rate of 500 MS/s. The blue trace shows the raw data. The middle trace (orange) and lower trace (red) show the effect of applying Boxcar Averaging functions to the raw data using 8 and 64 adjacent points respectively. Both of the averaged traces display visibly lower noise levels.
Improved Resolution and Dynamic Performance
To allow maximum flexibility the Spectrum Boxcar Averaging function allows users to select the number of adjacent points to be averaged from 2 to 256. The averaged data is subsequently stored with higher resolution by an amount that is proportional to the number of points selected. For example, selecting two adjacent points would increase the resolution of a 16 Bit digitizer to that equivalent to 17 Bits, selecting four adjacent points equates to 18 Bits and selecting the maximum 256 points would produce a theoretical 24 Bits! In reality, such high performance is never actually achieved for real signals. However, substantial measurement improvements can be made.
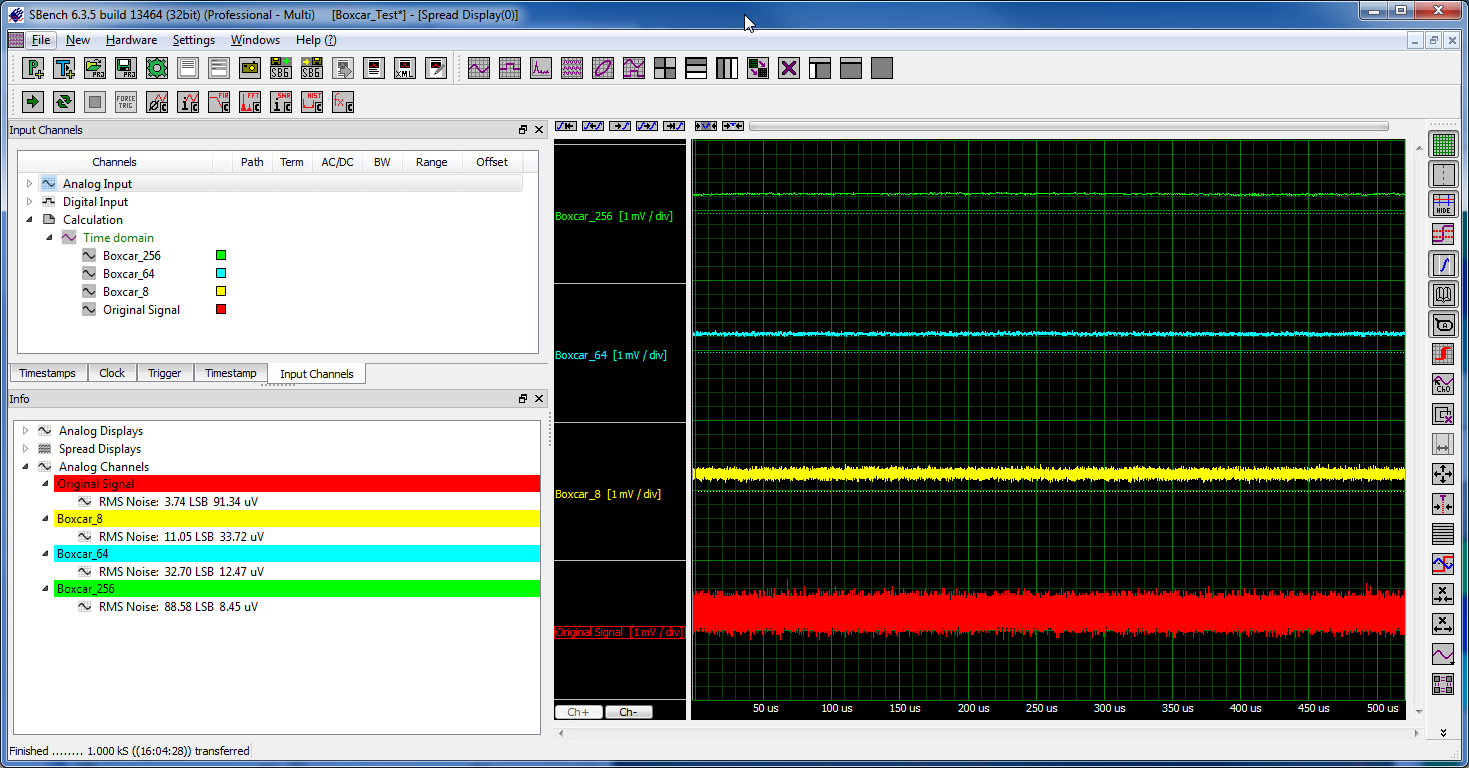 Figure 4 shows how well Boxcar Averaging can work to reduce the absolute noise floor of a signal. Here the lower trace (red) is an acquisition again made by an M4i.4451-x8 digitizer that is sampling at 500 MS/s and with 14 bit resolution. The trace shows the high noise floor that is observed when no signal is connected to the digitizer (effectively it has an open input). The RMS noise level is measured, with Spectrums SBench6 analysis software, and is shown in the "Info box" (lower left window) as being 91.34 µV. Applying a Boxcar Averaging function with factors of 8 (yellow trace) , 64 (blue trace) and 256 (green trace) results in a large decrease in the RMS noise. SBench6 shows the reduction as being 33.72, 12.47 and 8.45 µV respectively.
Figure 4 shows how well Boxcar Averaging can work to reduce the absolute noise floor of a signal. Here the lower trace (red) is an acquisition again made by an M4i.4451-x8 digitizer that is sampling at 500 MS/s and with 14 bit resolution. The trace shows the high noise floor that is observed when no signal is connected to the digitizer (effectively it has an open input). The RMS noise level is measured, with Spectrums SBench6 analysis software, and is shown in the "Info box" (lower left window) as being 91.34 µV. Applying a Boxcar Averaging function with factors of 8 (yellow trace) , 64 (blue trace) and 256 (green trace) results in a large decrease in the RMS noise. SBench6 shows the reduction as being 33.72, 12.47 and 8.45 µV respectively.
Not only does Boxcar Averaging reduce the effect of high noise levels on signals but, importantly, it improves the results in low noise level situations too. For example, when using high purity signals, tests show that Boxcar Averaging can improve a digitizer's performance, as measured by its ENOB, by at least 2 Bits. Other dynamic parameters, such as SFDR and SNR measurements, can also be increased by more than 12 dB. Table 1 shows the typical results achieved when measuring the dynamic performance parameters of the Spectrum M4i.4451-x8 digitizer when acquiring a high purity 1 MHz sine wave.
|
Standard Mode |
Boxcar 8x |
Boxcar 64x | |
|---|---|---|---|
|
SNR |
68.1 dB |
76.8 dB |
80.5 dB |
|
THD |
-80.1 dB |
-80.2 dB |
-82.0 dB |
|
SFDR excl. |
74.7 dB |
87.8 dB |
88.0 dB |
|
ENOB (SINAD) |
11.0 LSB |
12.2 LSB |
12.7 LSB |
|
ENOB (SNR) |
11.0 LSB |
12.5 LSB |
13.1 LSB |
What's the catch?
The downside of Boxcar averaging is that the resulting waveforms are effectively filtered so high-frequency signal content may be lost. The effective sampling rate is reduced by the Boxcar Averaging factor. The higher the factor the lower the sampling rate and the lower the resulting Nyquist frequency limit. However, even this can sometimes be an advantage. As the Boxcar Averaged waveform is decimated by the averaging factor so too is the stored waveform. The result is a waveform that requires less on-board memory and that can subsequently be transferred to a PC and processed faster. In addition, even though the resulting waveforms are decimated, the Spectrum implementation makes sure that the trigger detection is still running with full sampling speed of the original acquisition so that there is always a very precise timing relationship between the averaged signal and the trigger position.
Easy software integration
While the Boxcar Averaging mode is implemented with FPGA firmware it is fully programmable using Spectrums standard driver kit (SDK). The SDK allows programming with almost any popular language including C++, Visual Basic, VB.NET, C#, J#, Delphi, Java and Python. Third party software support and examples are also available, free of charge, for LabVIEW, LabWindows and MATLAB. For those users not wanting to write their own programs, Spectrum offers SBench 6-Pro, an easy-to-use, graphical user interface. SBench 6 provides control of all the digitizer's operating modes and settings. It displays, stores and processes waveforms and can even be used to document results.
Summary
In situations where the signals of interest are at frequencies that are well below the sampling rate of the digitizer then the Boxcar Averaging technique offers a number of advantages. Unlike traditional averaging methods, Boxcar Averaging works for single shot acquisitions. You don't need multiple trigger events or a repeatable signal. Furthermore, when signals are oversampled, Boxcar Averaging allows amplitude measurements to be made with more resolution as well as improving a digitizers overall ENOB, SNR and SFDR. Boxcar averaged waveforms are also decimated by the averaging factor. So, stored waveforms are reduced in size and can be transferred and processed faster.
Download
- Full article as pdf (English)